Se le llama así, cuadrado mágico, pues al construirlo se utilizaron los números del 1 al 9 y al sumar los elementos que se encuentran en sus columnas, filas o las dos diagonales, se obtiene siempre el mismo resultado de 15, que se le llama la suma mágica.
Pensemos ahora en el cuadrado de orden 4 que se obtiene colocando los números del 1 al 16 de la siguiente forma:
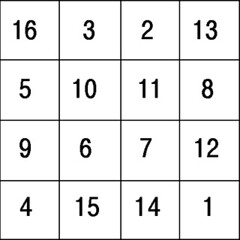
Se puede comprobar, para verificar que es un cuadrado mágico, que la suma de los elemento de las filas, columnas o las dos diagonales es el mismo valor de 34, su suma mágica. Este cuadrado fue incorporado por el pintor Alberto Durero en su ob
ra Melancolía, en la parte superior derecha de la obra y cumple algunas propiedades adicionales, como por ejemplo, incluye la fecha de la pintura en la parte inferior al centro, año 1514, la suma de las cuatro celdas centrales (10,11,6,7), las cuatro esquinas (16,13,4,1) y otras combinaciones simétricas, suman también 34, entre muchas otras propiedades, que le dan un carácter más que mágico a este cuadrado.
Debo decir que existen, aparte de los dados anteriormente, varios cuadrados de orden 3 y otros muchos de orden 4, y por supuesto entre mayor tomamos el orden o tamaño de este cuadrado, será mayor la dificultad de ordenar los números de manera que se cumpla que la suma de los elementos de cada fila, columna y diagonal sea la misma. Como dato interesante, para los de orden 4, De Bessy estableció en 1693 que existen 880 cuadrados mágicos distintos. Más adelante se ha demostrado que existen 275305224 cuadrados mágicos de orden 5. Para órdenes más grandes sólo se tienen estimaciones.
ra Melancolía, en la parte superior derecha de la obra y cumple algunas propiedades adicionales, como por ejemplo, incluye la fecha de la pintura en la parte inferior al centro, año 1514, la suma de las cuatro celdas centrales (10,11,6,7), las cuatro esquinas (16,13,4,1) y otras combinaciones simétricas, suman también 34, entre muchas otras propiedades, que le dan un carácter más que mágico a este cuadrado.Debo decir que existen, aparte de los dados anteriormente, varios cuadrados de orden 3 y otros muchos de orden 4, y por supuesto entre mayor tomamos el orden o tamaño de este cuadrado, será mayor la dificultad de ordenar los números de manera que se cumpla que la suma de los elementos de cada fila, columna y diagonal sea la misma. Como dato interesante, para los de orden 4, De Bessy estableció en 1693 que existen 880 cuadrados mágicos distintos. Más adelante se ha demostrado que existen 275305224 cuadrados mágicos de orden 5. Para órdenes más grandes sólo se tienen estimaciones.
El gran inventor estadounidense, Benjamin Franklin, encontró el cuadrado mágico de orden 8 dado por:
En donde cada fila, diagonal y columna suman 260, él mismo era apasionado por este tipo de problemas, que ocupaban sus horas de ocio mientras hacía las labores de oficinista en Filadelfia, como dato curioso, y evidencia de su genialidad, se cuenta que en una sola tarde, logró resolver el cuadrado de orden 16.
Leonard Euler, el más prolífico y gran matemático suizo encontró un cuadrado mágico de orden 8, en donde cada fila y cada columna suma 260, pero que además, cada fila y columna de cada uno de los cuatro subcuadrados de orden 4 que se obtienen, si partimos este cuadrado en cuatro, sumaba 130 y, adicionalmente, tal que en este "tablero mágico" de orden 8 se describe la ruta del movimiento del caballo por todo el tablero sin estar dos veces en ninguna de ellas conocido como el "problema del movimiento del caballo".
De las variaciones de los cuadrados mágicos, la que más me ha llamado la atención es el de orden 4 que se incorpora en La Fachada de la Pasión del Templo Expiatorio de la Sagrada Familia en Barcelona, monumental y alucinante obra de Antonio Gaudí, vemos en el beso de Judas:
De las variaciones de los cuadrados mágicos, la que más me ha llamado la atención es el de orden 4 que se incorpora en La Fachada de la Pasión del Templo Expiatorio de la Sagrada Familia en Barcelona, monumental y alucinante obra de Antonio Gaudí, vemos en el beso de Judas:
El criptograma de Gaudí, como lo llaman, ampliado es:
En este caso la constante mágica del cuadrado es 33, la edad de Jesucristo, para ello, dos de los números (el 12 y el 16) están disminuidos en dos unidades (10 y 14) con lo que aparecen dos repeticiones, de esta manera se logra rebajar la constante mágica en 1 unidad, de 34 a 33.
Esta suma mágica será siempre 33, en 310 combinaciones distintas en grupos de cuatro, solo por citar algunas: 1,14,11,7 (subcuadrado superior izquierdo) ó 8,10,13,2 (subcuadrado inferior izquierdo) ó 7,6,10,10 (subcuadrado interior) ó 14,11,6,2 (una cruz) ó 14,7,9,3 (una cruz) ó 14,6,10,3 (culebrilla) ó 11,8,9,5 ó 14,14,2,3, entre otras que usted mismo puede intentar por medio de figuras geométricas o recorridos.
De esta manera, podemos utilizar en nuestras aulas la magia de estos cuadrados para motivar a nuestros estudiantes y, de paso, evidenciar la gran relación que existe entre las matemáticas y el arte.
